Introduce Time Series Analysis with ARIMA (Part 2)

By Tsuyoshi Matsuzaki on 2017-08-04• ( 1 Comment )

Part 1 : AR, MA, ARMA (Stationary Model)
Part 2 : ARIMA, Seasonal ARIMA (Non-Stationary Model) <- this post

In my previous post, I have explained AR, MA, and ARMA under stationary condition.
In this post, I proceed to non-stationary models, ARIMA.

Many of real cases (stock price, sales revenue, etc) are non-stationary time series or mixed ones. However it’s also important to understand the idea of stationary model, because the idea of non-stationarity is based on the stationary model.

5. Non-Stationary Time Series

The idea of non-stationary model is :

Make the series of differences $\{y_1 - y_0, y_2 - y_1, \cdots , y_t - y_{t-1}\}$ .
Consider stationarity for these difference series.

If the difference series is stationary model given as ARMA(p, q), we can estimate the model of differences with methods in previous post, and we can then take the original $\{y_t\}$ . This model is called ARIMA (AutoRegressive Integrated Moving Average) model and it’s denoted by ARIMA(p, 1, q).
In general, ARIMA(p, d, q) is given by the definition as : the series of d-th order difference is ARMA(p, q).

As I have described in my previous post, all MA model is stationary. Therefore we can focus on AR part for considering non-stationary model.

Even though there exists a little difference between parameters $\phi$ in AR(1), the mathematical behavior will be vastly changed. (As I described in my previous post, AR(1) is stationary when $|\phi| < 1$ .)
Let’s see the following example (curve) for different $\theta$ in AR(1).

Sample of $\phi = 0.9$ (stationary)

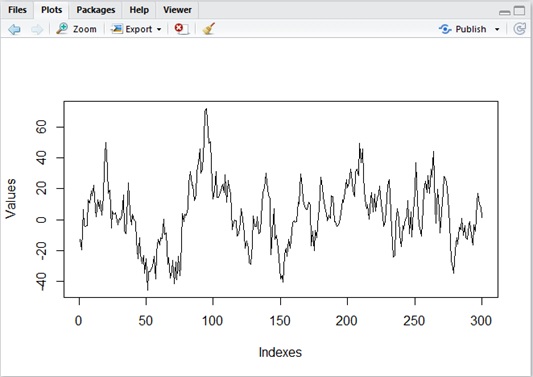
Sample of $\phi = 1.0$ (non-stationary)

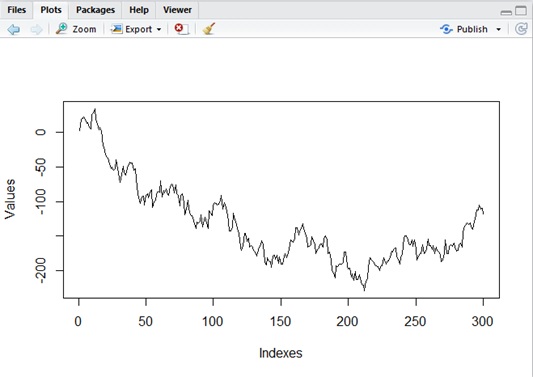
Sample of $\phi = 1.1$ (non-stationary)

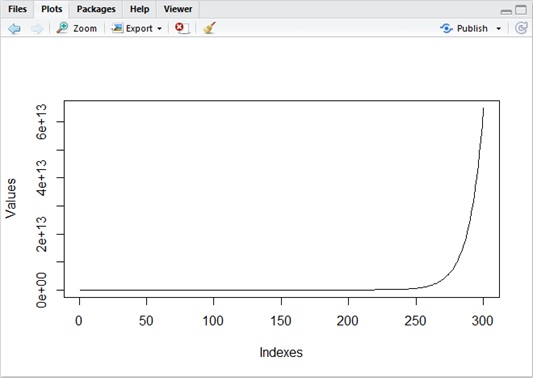
Unlike the stationary process, non-stationary process diverges in general. (See above in $\phi=1.1$ .)
Thus we cannot apply the same mathematical methods with stationary process for non-stationary one. Under the condition of non-stationarity, we cannot also use t-distribution (which is often used as statistical distribution) for estimation.

Now let’s see how we can estimate non-stationary model.

First we consider the following AR expression (1). (See my previous post for $\phi_k,\epsilon_t$ .)

$\displaystyle y_t = \phi_1 y_{t-1} + \phi_2 y_{t-2} + \cdots + \phi_p y_{t-p} + \epsilon_t \;\;\; (1)$

In this model, the following equation (2) is called “characteristic equation” :

$\displaystyle 1 - \phi_1 z - \phi_2 z^2 - \cdots - \phi_p z^p = 0 \;\;\; (2)$

It’s known that this equation follows the properties, such as :

If all the absolute values of roots of equation (2) are larger than 1, (1) is stationary.
If $z = 1$ is a root of $d$ multiplicity (i.e, the characteristic equation (2) has the term $(1 - z)^d$ in the factor) and the absolute values of other roots are all larger than 1, the series of d-th order difference of (1) is stationary.
Especially, if (2) has only one unit root (d = 1), the series of $y_t - y_{t-1}$ of (1) will become stationary.
This model is called unit root process.

Note : Later in this post, I’ll show you why this holds.

Now let’s start using the simple case of AR(1), which has the following equation.

$\displaystyle y_t = \phi_1 y_{t-1} + \epsilon_t$

In this case, we can find :

It’s stationary if $| \phi_1 | < 1$ .
It will be unit root process if $\phi_1 = 1$ .

If $\{y_t\}$ is stationary process (i.e, $| \phi_1 | < 1$ ), we can identify the model with methods in the previous post. If $\{y_t\}$ is unit root process (i.e, $\phi_1 = 1$ ), we can also identify the model, because $y_t - y_{t-1}$ is stationary process.
In general, you can repeat this process for series $\{ y_t - y_{t-1} \}$ , if neither of both.

Our next concern is : how to know whether it’s unit root process, when time series $\{y_0, y_1, \cdots, y_n\}$ is given.

6. Estimate Model and Forecast in ARIMA

Under the condition of unit root process, we cannot use t-distribution for estimation, because it is not stationary. Instead of that, we can use Dickey-Fuller test to distinguish whether model is unit root process.

Here (in this post) I don’t discuss details about Dickey-Fuller test, but the outline is below.
In order to simplify, I assume $y_k = y_{k-1} + \epsilon_k = \epsilon_1 + \epsilon_2 + \cdots + \epsilon_k$ here.:

Consider the following continuous stochastic process $X_n(t)$ , where $n$ is the size of given time series data and $\sigma$ is standard deviation of $\epsilon_t$ .
$\displaystyle X_n(t) = \frac{1}{\sqrt{n} \sigma} \left\{ \sum^{[nt]}_{i=1}\epsilon_i + (nt - [nt]) \epsilon_{[nt] + 1} \right\}\;\;\;(0 \leq t \leq 1)$
Intuitively, this will map $y_1,y_2,\cdots,y_n$ into $y = X_n(t)$ on the range $0 \leq t \leq 1$ separated by the segment of each spans $[\frac{i - 1}{n}, \frac{i}{n}] \; (i=1,2,\cdots,n)$ .
When $\{y_t\}$ is unit root process and $n$ is getting larger, it’s known that $X_n(t)$ converges to Wiener Process (Brownian Motion) on $[0,1]$ in stochastic distribution. (See “Donsker’s theorem“.)
Note that Wiener process $W(t)$ has properties $W(t + u) - W(t) \sim \mathcal{N}(0, u)$ and $W(0) = 0$ .
Then $W(1)$ is $\mathcal{N}(0,1)$ and $W(1)^2$ is $\mathcal{X}^2(1)$ .
It’s known that the following convergence with Wiener process holds, when $\{y_t\}$ is unit root process. (See “Continuous mapping theorem“.)
$\displaystyle \frac{|\hat{\phi_1} - \phi_1|}{SE_{\hat{\phi_1}}} = \frac{|\hat{\phi_1} - 1|}{SE_{\hat{\phi_1}}} \to \frac{1}{2} \cdot \frac{W(1)^2 - 1}{\sqrt{\int^1_0 W(t)^2 dt}} \;\;\;\;\; (3)$
where $\hat{\phi_1}$ is the least-squares estimator of $\phi_1$ , and $SE_{\hat{\phi_1}}$ is the standard error of least-squares estimator $\hat{\phi_1}$ .

This value (LHS of equation (3)) belongs to a specific distribution known as the Dickey–Fuller table, and you can then examine Dickey–Fuller test for finding whether it’s unit root process.
On contrary, it is known that the following value (t statistics) is on t-distribution table when $\{y_t\}$ is stationary. (See “Slope of a regression line” section in “Wikipeida : Student’s t-test“.)

Note : This describes Dickey-Fuller t-test for your understanding, but there also exists another Dickey-Fuller ρ-test.

There exists an extension of Dickey–Fuller test to AR(p), called Augmented Dickey–Fuller (ADF) test, and ADF test is used in practice.
Here I don’t describe details about this test (ADF), but with programming in R, you can simply use adf.test() (in tseries package) for running ADF test.

Now, let’s estimate the following time series data with linear positive trend in R script.

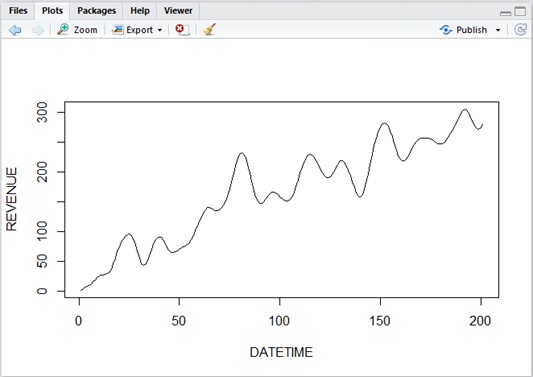
Same like the stationary model (see my previous post), you can simply use auto.arima() for identifying model and estimating parameters, also for ARIMA. (See below.)
You don’t need to follow previous steps in your programming code.

library(forecast)# read datay <- read.table(  "C:\Demo\revenue_sample.txt",  col.names = c("DATETIME", "REVENUE"),  header = TRUE,  quote = """,  fileEncoding="UTF-8",  stringsAsFactors = FALSE)# analyzetest = auto.arima(y$REVENUE)summary(test)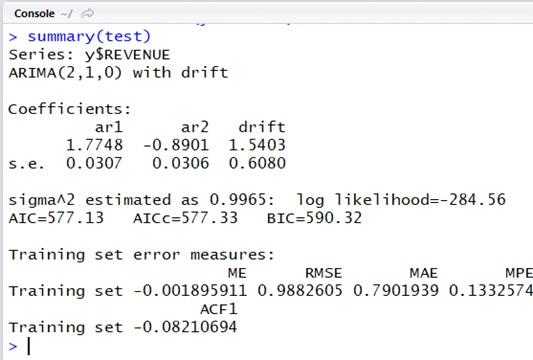

Here the obtained model of $\{ y_t \}_{t=1,2,\cdots}$ will be given as following equations.
The result “drift” (see the output above) means the trend of $y_t - y_{t-1}$ . (The meaning of “drift” will be near the gradient of $\{y_t\}$ .) In the following equation, 1.5403 is a drift value.

$\displaystyle y_t' - y_{t-1}' = 1.7748 \times (y_{t-1}' - y_{t-2}') - 0.8901 \times (y_{t-2}' - y_{t-3}') + \epsilon_t \;\;\; \epsilon_t \sim \mathcal{N}(0, 0.9965)$

and

$\displaystyle y_t = 1.5403 \times t + y_t'$

The following is the forecasting for the obtained model. (See below.)
Please compare the following predicted plotting (non-stationary result) with the one in my previous post (stationary result).
Unlike stationary model, the predicted mean (conditional mean) will not converge to the mean of model (it will always move by drift) and the predicted variance will also grow more and more.

...# analyzetest = auto.arima(y$REVENUE)summary(test)# predictpred <- forecast(  test,  level=c(0.85,0.95),  h=50)plot(pred)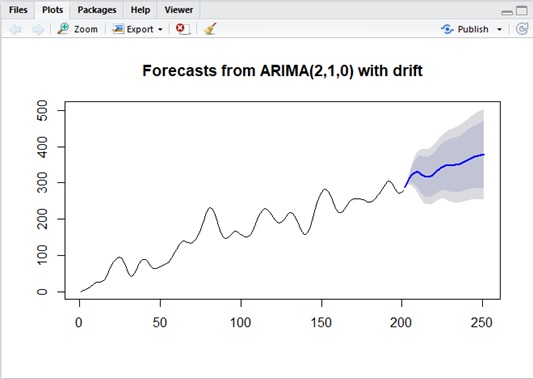

In auto.arima(), it will repeatedly test the difference $d$ for $0 \leq d \leq 2$ . Even if data has seasonality for large interval, it won’t test all possible difference.
In the next topic, I will discuss how these seasonality can be solved in ARIMA.

7. Backshift Notation

Before I discuss seasonal ARIMA, let me introduce convenient notation called “backshift notation”.

With this notation we denote $y_{t-1}$ by $B y_t$ . Of course, this doesn’t mean multiplying with some real number $B$ (i.e, $B \not\in \mathbb{R}$ ). It’s just the notation.
Same like this, $B^2 y_t$ means $y_{t-2}$ .

With this notation, the following transition holds.

$\displaystyle B^2 y_t = B (B y_{t-2}) = B y_{t-1} = y_{t-2}$

With this notation, we can easily treat the time series differences by such like arithmetic operations.
For example, $1 - B$ means the difference of sequence as follows.

$\displaystyle (1-B) y_t = y_t - B y_t = y_t - y_{t-1}$

$(1 - B)^2$ means the 2nd order difference as follows.

$\displaystyle (1-B)^2 y_t \\ = (1-B) (y_t - y_{t-1}) \\ = (1-B) y_t - (1-B) y_{t-1} \\ = y_t - y_{t-1} - y_{t-1} + y_{t-2} \\ = (y_t - y_{t-1}) - (y_{t-1} - y_{t-2})$

By repeating this operation, you can denote p-th order difference by $(1-B)^p$ .

With this notation, ARIMA(1,1,0) is denoted by the following equation, where $c$ is constant.

$\displaystyle (1 - \phi_1 B)(1 - B) y_t = c$

$\displaystyle y_t - y_{t-1} - \phi_1 y_{t-1} + \phi_1 y_{t-2} = c$

$\displaystyle y_t - y_{t-1} = \phi_1 (y_{t-1} - y_{t-2}) + c$

As you can see above, this notation clarifies the structure of model, because $(1 - \phi_1 B)$ means the part of AR(1), and $(1-B)$ means the part of $d = 1$ .
Thus, when you want to denote ARIMA(1,d,0), you can easily get by the following representation.

$\displaystyle (1 - \phi_1 B)(1 - B)^d y_t = c$

Now I rewrite the previous equation (1) with backshift notation as follows.

$\displaystyle y_t = \phi_1 y_{t-1} + \phi_2 y_{t-2} + \cdots + \phi_p y_{t-p} + \epsilon_t$

$\displaystyle y_t - \phi_1 y_{t-1} - \phi_2 y_{t-2} - \cdots - \phi_p y_{t-p} = \epsilon_t$

$\displaystyle (1 - \phi_1 B - \phi_2 B^2 - \cdots - \phi_p B^p) y_t = \epsilon_t$

As you can see above, LHS (left-hand-side) in the last expression is the same format with expression (2).
If (2) can be represented by $(1 - z)^d Y(z)$ and the absolute values of all roots in $Y(z)$ are larger than 1, the series of d-th order difference of (1) will be stationary, because this process will be written as follows. ( $Y(B)$ is stationary and $(1 - B)^d y_t$ is d-th order difference.)

$\displaystyle Y(B) (1 - B)^d y_t = \epsilon_t$

As you saw above, you can easily get the previous consequence with backshift notation.

8. Seasonal ARIMA (SARIMA)

With backshift notation, you can easily understand seasonal ARIMA model.
First, I’ll show you the basic concept using simple AR(1) model with no difference d.

Suppose, the sales revenue is so much affected by the revenue of the same month a year ago (12 months ago).
Then this relation can be written by the following expression with backshift notation. (For simplicity, I skipped the constant value $c$ in the expression.)

$\displaystyle (1 - \Phi_1 B^{12})y_t$

Note : $\Phi_1$ means the seasonal part of $\phi_1$ in AR. The upper letter is often used for seasonal part to distinguish with the non-seasonal part.

Suppose the revenue is also affected by the revenue from a month ago.
Then the mixed model will be represented as follows. This model is denoted by $ARIMA(1,0,0) \times (1,0,0)_{12}$ .

$\displaystyle (1 - \phi_1 B)(1 - \Phi_1 B^{12})y_t$

What does this model mean ? (Why it’s multiplied ?)

By transforming this representation, you will get the following :

$\displaystyle (y_t - \Phi_1 B^{12} y_t) - \phi_1 (y_{t-1} - \Phi_1 B^{12} y_{t-1})$

As you can see above, $y_t - \Phi_1 B^{12} y_t$ means the $t$ ‘s revenue, in which the effect of 12 months ago will be eliminated. Same like this, $y_{t-1} - \Phi_1 B^{12} y_{t-1}$ means the $(t - 1)$ ‘s revenue, in which the effect of 12 months ago will also be eliminated.
Therefore this expression means “AR(1) model for the effect of one month ago, in which the effect of 12 months ago is eliminated”.

This is also written by the following representation. As you can see, it’s vice versa.

$\displaystyle (y_t - \phi_1 B y_t) - \Phi_1 (y_{t-12} - \phi_1 B y_{t-12})$

I have showed the above sample with no differences so far, but when it has the difference $d$ , you just multiply $(1 - B)$ in backshift notation.
For example, $ARIMA(1,2,0) \times (1,3,0)_{12}$ is represented as follows :

$\displaystyle (1 - \phi_1 B)(1 - \Phi_1 B^{12})(1 - B)^2(1 - B^{12})^3 y_t$

In this expression :

$(1 - \phi_1 B)$ is AR(1) of non-seasonal part.
$(1 - \Phi_1 B^{12})$ is AR(1) of seasonal part.
$(1 - B)^2$ is the difference of non-seasonal part.
$(1 - B^{12})^3$ is the difference of seasonal part.

Note : If you have MA(1), you can write on RHS as follows. (In this post, I don’t discuss about MA part in seasonal ARIMA.)
$\displaystyle (1 - \phi_1 B)(1 - B)^2y_t = (1 + \theta_1 B)$

9. Find Seasonality

When I transform the equation of $ARIMA(1,0,0) \times (1,0,0)_{12}$ as follows, you can find that it is the same as ordinary ARIMA with lag 1, 12, and 13. (See below.)

$\displaystyle (1 - \phi_1 B)(1 - \Phi_1 B^{12})y_t \\ = y_t - \phi_1 y_{t-1} - \Phi_1 y_{t-12} + \phi_1 \Phi_1 y_{t-13}$

Suppose, we don’t know the seasonality for given time series data. Then we must estimate with all possible difference (lags) and coefficients $\phi_1, \phi_2, ..., \phi_{13}$ .
It will be time-consuming to search all possible lags. Please imagine if we have seasonality with seasonal lag = 365.

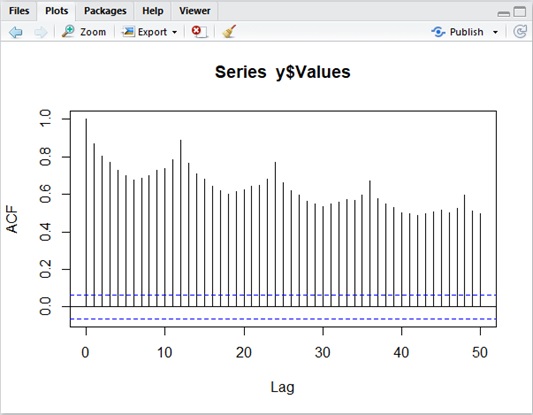
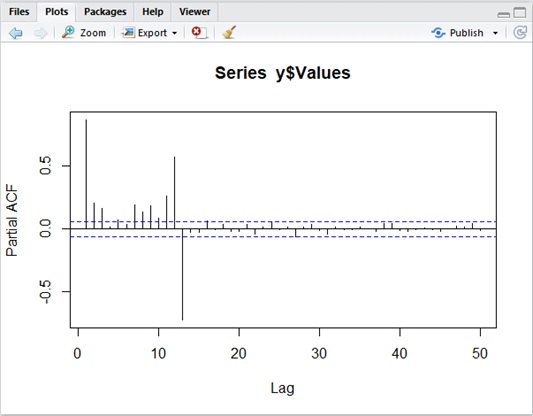
The following is ACF and PACF for $ARIMA(1,0,0) \times (1,0,0)_{12} (\phi = \Phi = 0.9)$ in R. (See my previous post about ACF and PACF.)
As you can see in the following result, it has the spike at lags in seasonal part. Thus ACF and PACF can also be used in order to identify a seasonal model.

Autocorrelation (ACF) sample

Partial Autocorrelation (PACF) sample

Let’s see the brief example in R.
Now I’ll start to estimate the model and forecast with the obtained model as usual.

library(forecast)# read datay <- read.table(  "C:\Demo\seasonal_sample.txt",  col.names = c("DATETIME", "REVENUE"),  header = TRUE,  fileEncoding="UTF-8",  stringsAsFactors = FALSE)# analyzetest <- auto.arima(y$REVENUE)summary(test)# predict and plotpred <- forecast(  test,  level=c(0.85,0.95),  h=100)plot(pred)

As I mentioned above, auto.arima() doesn’t test all possible lags.
Eventually I’ll get the result without seasonality (the result is ARIMA(0,1,1) with drift) as follows and the forecast plotting will become unexpected one.

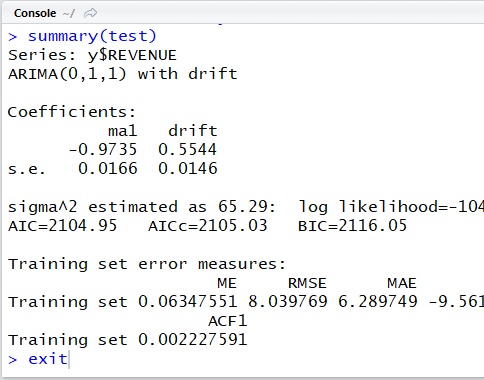
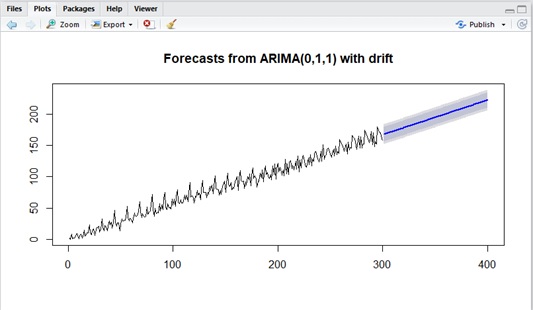
Suppose we test with ACF/PACF and know that this dataset has possible seasonality with lag 12 (for instance, 12 months).
Now we can fix the previous R script to use this known seasonality as follows. (Here I have changed the code in bold fonts.)

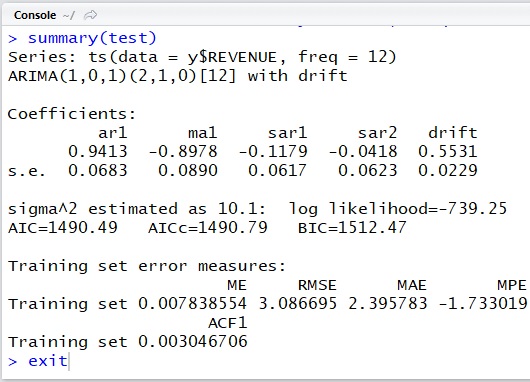
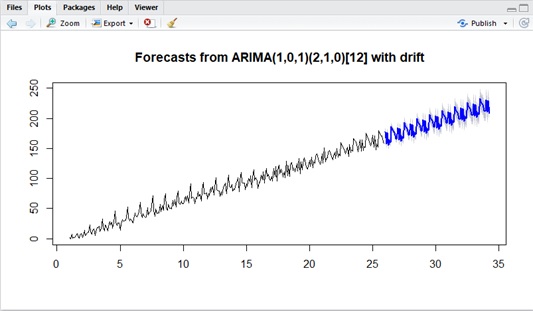
library(forecast)# read datay <- read.table(  "C:\Demo\seasonal_sample.txt",  col.names = c("DATETIME", "REVENUE"),  header = TRUE,  fileEncoding="UTF-8",  stringsAsFactors = FALSE)# analyze with seasonal s=12test <- auto.arima(ts(data=y$REVENUE, freq=12))summary(test)# predict and plotpred <- forecast(  test,  level=c(0.85,0.95),  h=100)plot(pred)

As you can see below, now we can get the desirable result with seasonal ARIMA.

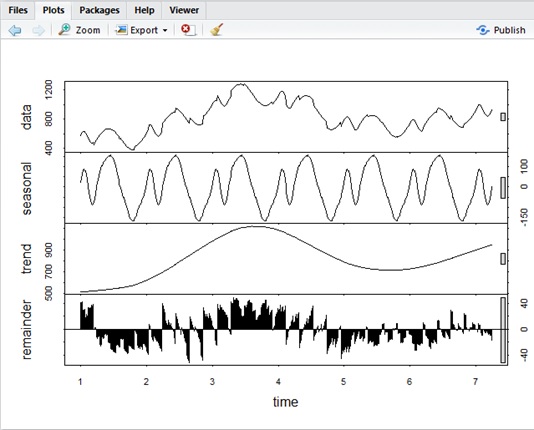
ARIMA doesn’t include the decomposition idea, but it’s sometimes useful to decompose and get properties (drift, seasonality) for time series data beforehand.
For instance, the following original data (“data” section in the following curves) is decomposed by stl() function in R as follows.

Categories: Uncategorized

Tagged as: MachineLearning

tsmatz

Professional Development, Data Science

Introduce Time Series Analysis with ARIMA (Part 2)

5. Non-Stationary Time Series

6. Estimate Model and Forecast in ARIMA

7. Backshift Notation

8. Seasonal ARIMA (SARIMA)

9. Find Seasonality

1 reply»

Leave a Reply Cancel reply

Recent Posts

Reinforcement Learning

Imitation Learning

Language Processing

Diffusion Models

Tags

Follow

Introduce Time Series Analysis with ARIMA (Part 2)

5. Non-Stationary Time Series

6. Estimate Model and Forecast in ARIMA

7. Backshift Notation

8. Seasonal ARIMA (SARIMA)

9. Find Seasonality

Share this:

Related

1 reply»

Leave a Reply Cancel reply

Recent Posts

Reinforcement Learning

Imitation Learning

Language Processing

Diffusion Models

Tags

Follow