(Download source code from here.)

For the last post of this series, I’ll show you the most famous quantum algorithm, Shor’s algorithm, with Q# implementation.

Series : Quantum algorithm’s implementation (Q#)

• Programming Quantum Algorithm for Beginners (Bernstein-Vazirani algorithm)
• Programming Quantum Search (Grover’s Algorithm)
• Programming Quantum Phase Estimation
• Programming Quantum Arithmetic (Adder, Multiplier, and Exponentiation)
• Programming Quantum Period Finding (Shor’s Algorithm)

In classical method, you needs exponential time computation (of the input’s bit size) for solving integer factorization, but you can solve with polynomial time computation by Shor’s algorithm.
This algorithm would have significant impacts for today’s computing, because current cryptographic technology depends on the difficulty of large composite integer’s factorization in classical approaches, and a lot of computing technologies (such as, security, identity, blockchain, etc) then depend on this current cryptographic technology.

Note : For this reason, quantum cryptography and key distribution (see here) is one of big concerns in today’s quantum studies and researches.

As well as other posts in this series, first I’ll describe the outline (idea) of this algorithm, and later I’ll show you Q# code along with this idea.

Before starting this post, I recommend you to read my early posts in this series (especially, “Quantum Fourier Transform (QFT) / Phase Estimation” and “Quantum Arithmetic“), if you’re not familiar with quantum methods.

Quantum Period-Finding (Shor’s Algorithm)

If positive integer and is coprime, number theory tells us there exists such as . We now assume that is positive least number such that .
As you can see :

Therefore is periodic (cyclic) for input by -cycle. (If there exists more least integer such that , this implies and is not then the least integer.)
For instance, if and , then equals to 5, 3, 4, 9, 1, 5, 3, 4, 9, 1, 5, 3, … In this case, the period length is 5.

…

This period is called “order” of modulus .

Our concern is how to find the period (order) for given coprime integers and .
Of course, you can iteratively search by calculating with to , but it needs computation time (i.e, exponential time), where the integer has bit’s size.
Here we want more efficient algorithms, and Peter Shor has showed us polynomial-time algorithm with quantum computer as follows.

The outline of Shor’s algorithm is : transform to all possible values using quantum superpositions, apply some modulus operations for these qubits, and then finally estimate the period using measured values.
Now let’s see the details of this algorithm and see why this makes things.

In this algorithm, we need the following 2 register :

• The first register has qubits, in which satisfies .
• The second register has at least qubits for storing .

To simplify explanation, here we assume that is some integer , i.e, . (Later we will discuss about the case in which is not an integer…)
Note that is unknown for now.

First we generate the superposition for . (i.e, )
Then the state of is now :

Next we transform (which is initialized by ) as follows.
For this implementation, please see my previous post “Quantum Arithmetic (Q#)“.

Now we measure the register . Once we’ve measured , the register is garbage and we don’t need any more.

After you’ve measured the register , results into for some .
Hence results into the following state, because .

Note : See here for quantum measurement.

Now we apply Quantum Fourier Transform (QFT) for register , and then results into the following state. (See this post for QFT.) :

Now let me fix some ( ) such that is not integer. In this case, the terms in the square brackets in the above equation cancels each others and then results into 0, because for some integer .
As a result, only terms with , in which is integer, resides in the above equation.

Next let me fix some ( ) such that is integer. In this case, equals to 1. And the number of such will then be , such as .
Therefore we can replace above equation with , and we then get :

Now we measure and assume that the results is some integer .

As you can easily see, we get for some unknown integer .
If and is coprime, you can get using greatest common divisor (shortly, GCD) by Euclidean algorithm with known and .

But it’s not so simple. Please remind our assumption : . For instance, when is odd, you cannot simply get by GCD.
When , it’s known that is approximated by the following using continued fraction expansion. If the following and is coprime, then you can get . If it’s not coprime (check if the result is an order or not), you repeat this algorithm until you find an order . (Here I don’t describe about this approximation, but please refer p.18 in the original paper “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer” by Peter Shor.)

where and

Note : For approximation, there exists another option, which uses phase estimation.
See “Applications – Shor’s Algorithm” in Q# document for details.

Number theory tells us that this takes place with probability at least (see Hardy-Ramanujan theorem), and the entire period-fining (order-finding) has computation complexity. That is, this algorithm has polynomial computation complexity of the input size .

Programming Quantum Period-Finding

Now let’s start Q# programming along with above algorithm.

Note : As I have mentioned in previous post, my code is written straightforward without any optimization, in order to help you understand the algorithm’s outline. (e.g, So many QFTs are called inside my function.)
Once you have learned core concept in this post, please proceed to optimize your code.

First we prepare the register and , which states are all initialized as .

// Get least integer n1 such as : num^2 <= 2^n1let n1 = BitSizeI(num) * 2;let n2 = BitSizeI(num);...use (x, y) = (Qubit[n1], Qubit[n2]) {  ...}

We apply and generate superposition as follows.

...use (x, y) = (Qubit[n1], Qubit[n2]) {  Microsoft.Quantum.Canon.ApplyToEachCA(H, x);  ...}

Next we apply in Q#.

In previous post, we’ve already learned and implemented this algorithms.
The following QuantumMultiplyByModulus() is the operation which I have already built in previous post.
The following QuantumExponentForPeriodFinding() is a modified version of QuantumExponentByModulus() in previous post.

...use (x, y) = (Qubit[n1], Qubit[n2]) {  Microsoft.Quantum.Canon.ApplyToEachCA(H, x);  // |x⟩ |0 (=y)⟩ -> |x⟩ |a^x mod N⟩  QuantumExponentForPeriodFinding(a, num, x, y);  ...}...

// Implement : |x⟩ |0 (=y)⟩ -> |x⟩ |a^x mod N⟩ for some integer a// (where y should be |0⟩)// This is modified version of QuantumExponentByModulus() in my post.// See /2019/05/22/quantum-computing-modulus-add-subtract-multiply-exponent/operation QuantumExponentForPeriodFinding (a : Int, N : Int, x : Qubit[], y : Qubit[]) : Unit {  let n1 = Length(x);  let n2 = Length(y);  // set |y⟩ = |0...01⟩  X(y[n2 - 1]);  for idx in 0 .. n1 - 1 {// a^(2^((n1-1) - idx)) is too big, then we reduce beforehandmutable a_mod = 1;for power in 1 .. 2^((n1-1) - idx) {  set a_mod = (a_mod * a) % N;}// apply decomposition elementsControlled QuantumMultiplyByModulus([x[idx]], (N, a_mod, y));  }}

Next we measure the register and apply Quantum Fourier Transform (QFT) to the register .
I note that the following QFTImpl() operation is the one which I have already built in this post. (You can also use Q# built-in operation for QFT.)

  ...// measure y and reset  mutable tmpResult = new Result[n2];  for idx in 0 .. n2 - 1 {set tmpResult w/= idx <-MResetZ(y[idx]);  }  // QFT for x  QFTImpl(x);  ...

Now we measure the register , and set results into variable “realResult“.

  // Measure x and reset  mutable realResult = new Result[n1];  for idx in 0 .. n1 - 1 {set realResult w/= idx <-MResetZ(x[idx]);  }

As I have mentioned above, we should get approximated fraction (where ) from the fraction (where is measured value, i.e, above “realResult“) by performing continued fraction expansion.
Here we use Microsoft.Quantum.Math.ContinuedFractionConvergentL() in Q# library for continued fraction, but you can also implement Euclidean by yourself. (We have also used Microsoft.Quantum.Math.GreatestCommonDivisorL() in Q# for GCD.)

  ...// get integer's result from measured array (ex : |011⟩ -> 3)  let resultBool = [false] + Microsoft.Quantum.Convert.ResultArrayAsBoolArray(realResult); // for making unsigned positive integer, add first bit  let resultBool_R = Microsoft.Quantum.Arrays.Reversed(resultBool); // because BoolArrayAsBigInt() is Little Endian order  let resultIntL = Microsoft.Quantum.Convert.BoolArrayAsBigInt(resultBool_R);  // get period candidate by continued fraction expansion (thanks to Euclid !)  let gcdL = GreatestCommonDivisorL(resultIntL, 2L^n1);  let calculatedNumerator = resultIntL / gcdL;  let calculatedDenominator = 2L^n1 / gcdL;  let numL = Microsoft.Quantum.Convert.IntAsBigInt(num);  let approximatedFraction =ContinuedFractionConvergentL(BigFraction(calculatedNumerator, calculatedDenominator), numL);  let (approximatedNumerator, approximatedDenominator) = approximatedFraction!;  mutable periodCandidateL = 0L;  if(approximatedDenominator < 0L) {set periodCandidateL = approximatedDenominator * -1L;  }  else {set periodCandidateL = approximatedDenominator; }  set periodCandidate = ReduceBigIntToInt(periodCandidateL);  // output for debugging  Message($"Measured Fraction : {resultIntL} / {2L^n1}");  Message($"Approximated Fraction : {approximatedNumerator} / {approximatedDenominator}");  Message($"Period Candidate : {periodCandidate}");  ...

// This is helper function to convert BigInt to Int ...operation ReduceBigIntToInt(numL : BigInt) : Int {  // Check if numL is not large  Microsoft.Quantum.Diagnostics.Fact(BitSizeL(numL) <= 32, $"Cannot convert to Int. Input is too large");  mutable resultInt = 0;  let numArray = Microsoft.Quantum.Convert.BigIntAsBoolArray(numL);  let numArray_R = Microsoft.Quantum.Arrays.Reversed(numArray); // because BigIntAsBoolArray() is Little Endian order  let nSize = Length(numArray_R);  for idx in 0 .. nSize - 1 {if(numArray_R[idx] and ((nSize - 1) - idx <= 31)) {  set resultInt = resultInt + (2 ^ ((nSize - 1) - idx));}  }  return resultInt;}

Finally you check if (above “periodCandidate”) is the period or not. If not, please repeat once again.

The completed Q# code is as follows.

open Microsoft.Quantum.Intrinsic;open Microsoft.Quantum.Math;open Microsoft.Quantum.Measurement;operation QuantumPeriodFinding (num : Int, a : Int) : Unit {  // Get least integer n1 such as : num^2 <= 2^n1  let n1 = BitSizeI(num) * 2;  let n2 = BitSizeI(num);  mutable periodCandidate = 1;  repeat {use (x, y) = (Qubit[n1], Qubit[n2]) {  Microsoft.Quantum.Canon.ApplyToEachCA(H, x);  // |x⟩ |0 (=y)⟩ -> |x⟩ |a^x mod N⟩  QuantumExponentForPeriodFinding(a, num, x, y);  // measure y and reset  mutable tmpResult = new Result[n2];  for idx in 0 .. n2 - 1 {set tmpResult w/= idx <-MResetZ(y[idx]);  }  // QFT for x  QFTImpl(x);  // Measure x and reset  mutable realResult = new Result[n1];  for idx in 0 .. n1 - 1 {set realResult w/= idx <-MResetZ(x[idx]);  }// get integer's result from measured array (ex : |011⟩ -> 3)  let resultBool = [false] + Microsoft.Quantum.Convert.ResultArrayAsBoolArray(realResult); // for making unsigned positive integer, add first bit  let resultBool_R = Microsoft.Quantum.Arrays.Reversed(resultBool); // because BoolArrayAsBigInt() is Little Endian order  let resultIntL = Microsoft.Quantum.Convert.BoolArrayAsBigInt(resultBool_R);  // get period candidate by continued fraction expansion (thanks to Euclid !)  let gcdL = GreatestCommonDivisorL(resultIntL, 2L^n1);  let calculatedNumerator = resultIntL / gcdL;  let calculatedDenominator = 2L^n1 / gcdL;  let numL = Microsoft.Quantum.Convert.IntAsBigInt(num);  let approximatedFraction =ContinuedFractionConvergentL(BigFraction(calculatedNumerator, calculatedDenominator), numL);  let (approximatedNumerator, approximatedDenominator) = approximatedFraction!;  mutable periodCandidateL = 0L;  if(approximatedDenominator < 0L) {set periodCandidateL = approximatedDenominator * -1L;  }  else {set periodCandidateL = approximatedDenominator; }  set periodCandidate = ReduceBigIntToInt(periodCandidateL);  // output for debugging  Message($"Measured Fraction : {resultIntL} / {2L^n1}");  Message($"Approximated Fraction : {approximatedNumerator} / {approximatedDenominator}");  Message($"Period Candidate : {periodCandidate}");}  }  until ((periodCandidate != 0) and (ExpModI(a, periodCandidate, num) == 1))  fixup {  }  // output for debugging  Message("Found period " + Microsoft.Quantum.Convert.IntAsString(periodCandidate));  Message("");}// Implement : |x⟩ |0 (=y)⟩ -> |x⟩ |a^x mod N⟩ for some integer a// (where y should be |0⟩)// This is modified version of QuantumExponentByModulus() in my post.// See /2019/05/22/quantum-computing-modulus-add-subtract-multiply-exponent/operation QuantumExponentForPeriodFinding (a : Int, N : Int, x : Qubit[], y : Qubit[]) : Unit {  let n1 = Length(x);  let n2 = Length(y);  // set |y⟩ = |0...01⟩  X(y[n2 - 1]);  for idx in 0 .. n1 - 1 {// a^(2^((n1-1) - idx)) is too big, then we reduce beforehandmutable a_mod = 1;for power in 1 .. 2^((n1-1) - idx) {  set a_mod = (a_mod * a) % N;}// apply decomposition elementsControlled QuantumMultiplyByModulus([x[idx]], (N, a_mod, y));  }}// This is helper function to convert BigInt to Int ...operation ReduceBigIntToInt(numL : BigInt) : Int {  // Check if numL is not large  Microsoft.Quantum.Diagnostics.Fact(BitSizeL(numL) <= 32, $"Cannot convert to Int. Input is too large");  mutable resultInt = 0;  let numArray = Microsoft.Quantum.Convert.BigIntAsBoolArray(numL);  let numArray_R = Microsoft.Quantum.Arrays.Reversed(numArray); // because BigIntAsBoolArray() is Little Endian order  let nSize = Length(numArray_R);  for idx in 0 .. nSize - 1 {if(numArray_R[idx] and ((nSize - 1) - idx <= 31)) {  set resultInt = resultInt + (2 ^ ((nSize - 1) - idx));}  }  return resultInt;}

You can invoke this code (Q#) from your Python code as follows. (Use Python or .NET .)

N = 11a = 5res = QuantumPeriodFinding.simulate(num=N, a=a)N = 15a = 7res = QuantumPeriodFinding.simulate(num=N, a=a)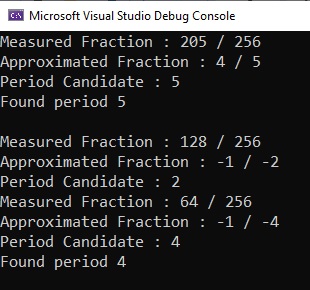

You can download and run source code from here.

Integer Factorization

Using above period-finding algorithm, we can now extend to integer factorization, which is also difficult to be solved by classical efficient algorithms.

Note : As you can easily see, it needs when you apply the trivial iteration search for integer factorization, where the integer has bit’s size. There exist several challenges (studies) for reducing computation complexity with classical algorithms, but it is known that there’s no existence with -polynomial complexity for a -bits number in classical algorithms. (See “Integer factorization” in Wikipedia.)

When is even and , it’s known that at least one of is a non-trivial factor of . Then overall algorithm of integer factorization for integer is as follows. :
(The following step 5 is quantum step, and others are classical.)

1. If is even, return 2 as a factor.
   If not, proceed to the next step.
2. Check if for some integer and . (Check for all . This will be -polynomial computation for -bit’s integer .)
   If so, return as a factor. Otherwise, proceed to the next step.
3. Pick a random integer and get the great common divisor with Euclidean algorithm.
4. If , return as a factor.
   If not, proceed to the next step.
5. If , and is coprime and then run above quantum period-finding algorithm for and . (i.e, find the least integer such as .)
6. If the period is odd, go back to step 3.
7. If the period is even and , go back to step 3.
8. Otherwise, check if is a nontrivial factor of . If not, go back to step 3.

Please try to implement quantum-inspired integer factorization with the combination of quantum part (above Q# code) and classical part (Python code).
(Here I skip this implementation example.)

In today’s gate-model quantum computers, there exist difficulties for error correction (correction of quantum noise) and fault tolerance, and the scaling up qubits (i.e, adding more qubits) will then increase the errors more.
Considering these facts, Shor’s algorithm for large number is hard to be implemented in today’s devices, and unfortunately example in this post will then be only for experimental purpose. (It won’t be applicable to the real business.)

We hope that we can make use of general-purpose (gate-model) quantum computers in the near future.

Reference :

Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer

Principles of Quantum Computation and Information