(Please download source code from here.)

Microsoft SEAL is a homomorphic encryption (HE) library, developed by Microsoft Research.

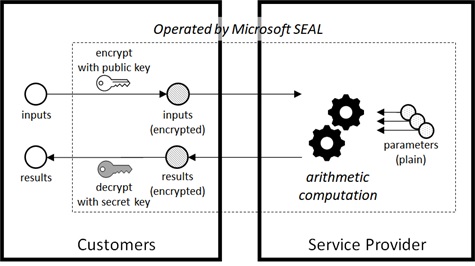
With homomorphic encryption (HE), the encrypted item can be used on computation without decryption. For sensitive data (such as, privacy data in healthcare), the customers can operate their own data without submitting private text to cloud service providers. (See below.)

Before staring, you should take care for the following description in Microsoft SEAL documentation.

“Microsoft SEAL is a homomorphic encryption library that allows additions and multiplications to be performed on encrypted integers or real numbers. Other operations, such as encrypted comparison, sorting, or regular expressions, are in most cases not feasible to evaluate on encrypted data using this technology. Therefore, only specific privacy-critical cloud computation parts of programs should be implemented with Microsoft SEAL.”

As this document says, not all parts in computation can be performed by HE manner, but you can separate and operate privacy-critical computation parts in Microsoft SEAL.

In this post, I’ll show you examples for operating primitive addition and multiplication in machine learning inferencing.

Note : There exists another open source software library to operate homomorphic encryption, HEAAN.

Install and Set Up Microsoft SEAL

Essentially, Microsoft SEAL is a library built on C++ (native), and it can also be used on .NET (C#) through a native C wrapper.
In this example,

1. In the first example, I will run SEAL computation on Python through this C wrapper functions to understand primitive SEAL functions.
2. In the next example, I will use EVA compiler (and PyEVA package) to simplify HE programming.

Now, let’s install Microsoft SEAL on Ubuntu. (Here I used Ubuntu 20.04 LTS on Microsoft Azure.)

First of all, we should install Clang++, g++, and cmake for building Microsoft SEAL.
See readme for the required version of Clang++, g++, and cmake.

sudo apt-get updatesudo apt install -y clangsudo apt install -y g++sudo apt install -y cmake

Note : To check versions in your platform, run as follows.

clang++ --versiong++ --versioncmake --version

Clone Microsoft SEAL repository to download source code.

git clone -b v3.7.2 https://github.com/microsoft/SEAL.git

Run as follows and build (compile) Microsoft SEAL.
By the following SEAL_BUILD_SEAL_C compiler option, C wrapper (libsealc.so.3.7.2) is also built as a shared library.

cd SEAL/cmake -S . -B build -DSEAL_BUILD_SEAL_C=ONcmake --build build

The output binaries will reside in build/lib/ directory.
In the following example, I’ll use libsealc.so.3.7.2 (C wrapper library), but use libsealc.so if you need version resilience. (Both libsealc.so and libsealc.so.3.7 are symbolic links for this library.)

ls build/lib/

libseal-3.7.a  libsealc.so  libsealc.so.3.7  libsealc.so.3.7.2  libz.a  libzstd.a

Run Computation in Microsoft SEAL (Python)

In order to understand SEAL primitive functions and fundamentals, let’s create a simple exmaple, which computes the following formula.
In this computation, both and results will be encrypted.

for .

SEAL implements 2 homomorphic encryption scheme, BFV (Brakerski/Fan-Vercauteren) and CKKS (Cheon-Kim-Kim-Song).
BFV scheme can operate only unsigned integer data types, and I then apply CKKS scheme in this example, which can operate the encrypted real and complex numbers. (See here for BFV programming with C wrapper.)

In this first example, I’ll perform computations in Python with SEAL native C wrapper’s functions.
Then, first you should load C wrapper functions as follows.

## Load C wrapper#import ctypesseal_lib = ctypes.CDLL("./SEAL/build/lib/libsealc.so.3.7.2")## Define native function's arguments#seal_lib.EncParams_Create1.argtypes = [ ctypes.c_byte, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.EncParams_SetPolyModulusDegree.argtypes = [ ctypes.c_void_p, ctypes.c_ulonglong ]seal_lib.EncParams_SetCoeffModulus.argtypes = [ ctypes.c_void_p, ctypes.c_ulonglong, ctypes.POINTER(ctypes.c_ulonglong) ]seal_lib.CoeffModulus_Create.argtypes = [ ctypes.c_ulonglong, ctypes.c_ulonglong, ctypes.POINTER(ctypes.c_int), ctypes.POINTER(ctypes.c_ulonglong) ]seal_lib.SEALContext_Create.argtypes = [ ctypes.c_void_p, ctypes.c_bool, ctypes.c_int, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.SEALContext_FirstParmsId.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_ulonglong) ]seal_lib.KeyGenerator_Create1.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.KeyGenerator_SecretKey.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.KeyGenerator_CreatePublicKey.argtypes = [ ctypes.c_void_p, ctypes.c_bool, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.KeyGenerator_CreateRelinKeys.argtypes = [ ctypes.c_void_p, ctypes.c_bool, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.CKKSEncoder_Create.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.CKKSEncoder_SlotCount.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_ulonglong) ]seal_lib.CKKSEncoder_Encode1.argtypes = [ ctypes.c_void_p, ctypes.c_ulonglong, ctypes.POINTER(ctypes.c_double), ctypes.POINTER(ctypes.c_ulonglong), ctypes.c_double, ctypes.c_void_p, ctypes.c_void_p ]seal_lib.CKKSEncoder_Encode3.argtypes = [ ctypes.c_void_p, ctypes.c_double, ctypes.POINTER(ctypes.c_ulonglong), ctypes.c_double, ctypes.c_void_p, ctypes.c_void_p ]seal_lib.CKKSEncoder_Decode1.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.POINTER(ctypes.c_ulonglong), ctypes.POINTER(ctypes.c_double), ctypes.c_void_p ]seal_lib.Plaintext_Create1.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.Encryptor_Create.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.Encryptor_Encrypt.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p ]seal_lib.Ciphertext_Create1.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.Ciphertext_SaveSize.argtypes = [ ctypes.c_void_p, ctypes.c_ubyte, ctypes.POINTER(ctypes.c_ulonglong) ]seal_lib.Ciphertext_Save.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_ubyte), ctypes.c_ulonglong, ctypes.c_ubyte, ctypes.POINTER(ctypes.c_ulonglong) ]seal_lib.Ciphertext_Scale.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_double) ]seal_lib.Ciphertext_SetScale.argtypes = [ ctypes.c_void_p, ctypes.c_double ]seal_lib.Ciphertext_ParmsId.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_ulonglong) ]seal_lib.Serialization_ComprModeDefault.argtypes = [ ctypes.POINTER(ctypes.c_ubyte) ]seal_lib.Evaluator_Create.argtypes = [ ctypes.c_void_p, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.Evaluator_Square.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p ]seal_lib.Evaluator_RescaleToNext.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p ]seal_lib.Evaluator_Multiply.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p ]seal_lib.Evaluator_MultiplyPlain.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p ]seal_lib.Evaluator_AddPlain.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p ]seal_lib.Evaluator_ModSwitchTo2.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.POINTER(ctypes.c_ulonglong), ctypes.c_void_p ]seal_lib.Decryptor_Create.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.POINTER(ctypes.c_void_p) ]seal_lib.Decryptor_Decrypt.argtypes = [ ctypes.c_void_p, ctypes.c_void_p, ctypes.c_void_p ]

Note : For available functions, see header files (.h files) in SEAL/native/src/seal/c/.

Then you should create SEAL context with encryption parameter.
In the following code, the larger PolyModulusDegree makes the size of ciphertext larger (i.e, more secure) and operations will then become slower. (This value must be a positive power of 2.)
An upper bound for the total bit-length of CoeffModulus is limited by the value of this PolyModulusDegree. For exampe, when PolyModulusDegree=8192, the size of maximum bit is 218. (Use CoeffModulus_MaxBitCount() to see the maximum size.)
Then I have set 5 40-bits prime numbers (total 200 bits) in CoeffModulus as follows. (Later I’ll explain why I set 40-bits for each prime.)

## Create encryption parameter (CKKS)#ptr_encparm = ctypes.c_void_p()seal_lib.EncParams_Create1(  ctypes.c_byte(0x02), # 0x02 means CKKS  ctypes.byref(ptr_encparm))## Set encryption parameter's attribute## 1. Set PolyModulusDegreeseal_lib.EncParams_SetPolyModulusDegree(  ptr_encparm,  ctypes.c_ulonglong(8192))# 2. Create CoeffModulus# (Here I create 5 40-bits prime numbers.)coeff_size_arr = (ctypes.c_int * 5)()coeff_size_arr[0] = 40coeff_size_arr[1] = 40coeff_size_arr[2] = 40coeff_size_arr[3] = 40coeff_size_arr[4] = 40coeff_arr = (ctypes.c_ulong * 5)()seal_lib.CoeffModulus_Create(  ctypes.c_ulonglong(8192),  ctypes.c_ulonglong(5),  ctypes.cast(coeff_size_arr, ctypes.POINTER(ctypes.c_int)),  ctypes.cast(coeff_arr, ctypes.POINTER(ctypes.c_ulong)))# 3. Set CoeffModulusseal_lib.EncParams_SetCoeffModulus(  ptr_encparm,  ctypes.c_ulonglong(5),  ctypes.cast(coeff_arr, ctypes.POINTER(ctypes.c_ulong)))## Create SEAL context# with encryption parameter## Createptr_context = ctypes.c_void_p()seal_lib.SEALContext_Create(  ptr_encparm,  ctypes.c_bool(True),  ctypes.c_int(128),  ctypes.byref(ptr_context))# Get first parms idparms_id = ctypes.c_ulonglong()seal_lib.SEALContext_FirstParmsId(  ptr_context,  ctypes.byref(parms_id))

Next I generate 3 keys – public key, secret key, relinearization key (relin key).
The public key is used for encryption and the secret key is for decryption. The relinearization key (relin key) is used in relinearization operations. (Later I’ll explain about relinearization operations.)

Therefore, the secret key should not be shared in public and held in customer side.

## Create keys for encryption, decryption, and relinearization## Create key generatorptr_key_generator = ctypes.c_void_p()seal_lib.KeyGenerator_Create1(  ptr_context,  ctypes.byref(ptr_key_generator))# Get secret key used for decryption# (Use SecretKey_Data() when you show secret key text)ptr_secret_key = ctypes.c_void_p()seal_lib.KeyGenerator_SecretKey(  ptr_key_generator,  ctypes.byref(ptr_secret_key))# Create public key used for encryptionptr_public_key = ctypes.c_void_p()seal_lib.KeyGenerator_CreatePublicKey(  ptr_key_generator,  ctypes.c_bool(False),  ctypes.byref(ptr_public_key))# Create relinearization key used for relinearizationptr_relin_key = ctypes.c_void_p()seal_lib.KeyGenerator_CreateRelinKeys(  ptr_key_generator,  ctypes.c_bool(False),  ctypes.byref(ptr_relin_key))

In CKKS scheme, the complex number is encoded into polynomials (see the original paper for CKKS encode), and this can be achieved with CKKSEncoder object in Microsoft SEAL.
Now I perform encoding for scalar values (in this example, 3.14159265 and 0.5) with CKKSEncoder object.

In this example, the number of generated slot (slot_size) will be 4096, and you can use a vector with 4096 elements. When you define values of 3.14159265 and 0.5 as follows, these scalar values will be encoded to every 4096 slots.
I note that these numbers will not be encrypted, and these are then Plaintext objects.

## Create CKKS encoder## Create CKKS encoderptr_encoder = ctypes.c_void_p()seal_lib.CKKSEncoder_Create(  ptr_context,  ctypes.byref(ptr_encoder))# In CKKS, the number of slots is PolyModulusDegree / 2 and each slot encodes one number.# In encryption, the encoder will implicitly pad it with zeros to full size, PolyModulusDegree / 2.slot_size = ctypes.c_ulonglong()seal_lib.CKKSEncoder_SlotCount(  ptr_encoder,  ctypes.byref(slot_size))## Create plaintexts for PI (3.14159265) and 0.5# with CKKS encoder# (Encodes these floating-point values to every slot)## Scale S = 2^40scale = pow(2.0, 40)# Create plain text for PIptr_plain_pi = ctypes.c_void_p()seal_lib.Plaintext_Create1(  None,  ctypes.byref(ptr_plain_pi))# CKKS encode for PIseal_lib.CKKSEncoder_Encode3(  ptr_encoder,  ctypes.c_double(3.14159265),  ctypes.byref(parms_id),  ctypes.c_double(scale),  ptr_plain_pi,  None)# Create plain text for 0.5ptr_plain_05 = ctypes.c_void_p()seal_lib.Plaintext_Create1(  None,  ctypes.byref(ptr_plain_05))# CKKS encode for 0.5seal_lib.CKKSEncoder_Encode3(  ptr_encoder,  ctypes.c_double(0.5),  ctypes.byref(parms_id),  ctypes.c_double(scale),  ptr_plain_05,  None)

Note : I’ll explain about “scale” setting (see above) later. (Please ignore for scaling here.)

Now I set 4 values (0.0, 1.1, 2.2, 3.3) of in slots, and other slots will then be padded with zeros.
These 4 values will also be encoded by CKKSEncoder object, but these are encrypted as Ciphertext object (not Plaintext object).

Here I don’t describe about steps, but you can serialize this cipher text and pass this object across network. (See here for Base64 encoding.)

## Create encryption for x (= 0.0, 1.1, 2.2, 3.3)# with CKKS encoder# (Other slots will be padded with zeros)## Create plain text for xptr_plain_x = ctypes.c_void_p()seal_lib.Plaintext_Create1(  None,  ctypes.byref(ptr_plain_x))# CKKS encode for xx_arr = (ctypes.c_double * 4)()x_arr[0] = 0.0x_arr[1] = 1.1x_arr[2] = 2.2x_arr[3] = 3.3seal_lib.CKKSEncoder_Encode1(  ptr_encoder,  ctypes.c_ulonglong(4),  ctypes.cast(x_arr, ctypes.POINTER(ctypes.c_double)),  ctypes.byref(parms_id),  ctypes.c_double(scale),  ptr_plain_x,  None)# Create cipher text for xptr_cipher_x = ctypes.c_void_p()seal_lib.Ciphertext_Create1(  None,  ctypes.byref(ptr_cipher_x))# Create encryptorptr_encryptor = ctypes.c_void_p()seal_lib.Encryptor_Create(  ptr_context,  ptr_public_key,  None,  ctypes.byref(ptr_encryptor))# Encrypt for xseal_lib.Encryptor_Encrypt(  ptr_encryptor,  ptr_plain_x,  ptr_cipher_x,  None)

Note : Use CKKSEncoder_Encode2() for complex numbers. (In this example, I operate only for real numbers.)

Next I compute in this context as follows.
The computation operation is performed by Evaluator object in Microsoft SEAL.

## Compute x^2## Create Evaluatorptr_evaluator = ctypes.c_void_p()seal_lib.Evaluator_Create(  ptr_context,  ctypes.byref(ptr_evaluator))# Create cipher text for resultptr_cipher_res1 = ctypes.c_void_p()seal_lib.Ciphertext_Create1(  None,  ctypes.byref(ptr_cipher_res1))# Square xseal_lib.Evaluator_Square(  ptr_evaluator,  ptr_cipher_x,  ptr_cipher_res1,  None)

Now I should explain about relinearization and scaling.

• Relinearization :
  When you apply multiplication by cipher text, the size of a cipher text will grow from 2 to 3. By reducing the size of a cipher text before the next multiplication, both noise growth and performance can be improved positively.
  The relinearization operation can be used to reduce the size of a cipher text, from size 3 down to size 2 (i.e, initial size).
• Rescaling :
  The scale in CKKS determines the bit-precision of the encoding and affects the precision of the result.
  If the cipher text has scale (in this example, I set 40 for initial scale), it’ll have scale after multiplication. When the primes in the CoeffModulus is (in this example, I also set 40 for primes), it will approximately be after rescaling.

For these reasons, we should perform both relinearization and rescaling, before next multiplication.
Note that relinearization itself has also significant computational cost, and you should design to minimize relinearization in practice.

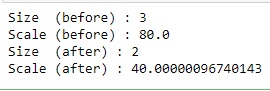
import math## Print size and scale of cipher#cipher_size = ctypes.c_ulonglong()seal_lib.Ciphertext_Size(  ptr_cipher_res1,  ctypes.byref(cipher_size))cipher_scale = ctypes.c_double()seal_lib.Ciphertext_Scale(  ptr_cipher_res1,  ctypes.byref(cipher_scale))print("Size  (before) : {}".format(cipher_size.value))print("Scale (before) : {}".format(math.log(cipher_scale.value, 2)))## Relinearize#seal_lib.Evaluator_Relinearize(  ptr_evaluator,  ptr_cipher_res1,  ptr_relin_key,  ptr_cipher_res1,  None)## Rescale#seal_lib.Evaluator_RescaleToNext(  ptr_evaluator,  ptr_cipher_res1,  ptr_cipher_res1,  None)## Print size and scale of cipher again#seal_lib.Ciphertext_Size(  ptr_cipher_res1,  ctypes.byref(cipher_size))seal_lib.Ciphertext_Scale(  ptr_cipher_res1,  ctypes.byref(cipher_scale))print("Size  (after) : {}".format(cipher_size.value))print("Scale (after) : {}".format(math.log(cipher_scale.value, 2)))

Here we cannot multiply to compute , because these have different scales. (See above result.)
Thus I compute , and then multiply and to get .
(In the following code, I have also rescaled after multiplication.)

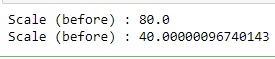
## Compute 3.14159265 x## Create cipher for the result of 3.14159265 xptr_cipher_res2 = ctypes.c_void_p()seal_lib.Ciphertext_Create1(  None,  ctypes.byref(ptr_cipher_res2))# Compute 3.14159265 xseal_lib.Evaluator_MultiplyPlain(  ptr_evaluator,  ptr_cipher_x,  ptr_plain_pi,  ptr_cipher_res2,  None)# Print scale of cipherseal_lib.Ciphertext_Scale(  ptr_cipher_res2,  ctypes.byref(cipher_scale))print("Scale (before) : {}".format(math.log(cipher_scale.value, 2)))# Rescale to set appropriate scaleseal_lib.Evaluator_RescaleToNext(  ptr_evaluator,  ptr_cipher_res2,  ptr_cipher_res2,  None)# Print scale of cipherseal_lib.Ciphertext_Scale(  ptr_cipher_res2,  ctypes.byref(cipher_scale))print("Scale (before) : {}".format(math.log(cipher_scale.value, 2)))

Now we can multiply and .

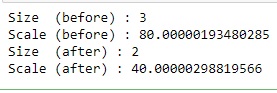
## Compute 3.14159265 x^3# by mutiplying x^2 and 3.14159265 x## Multiply x^2 and 3.14159265 xseal_lib.Evaluator_Multiply(  ptr_evaluator,  ptr_cipher_res1,  ptr_cipher_res2,  ptr_cipher_res2,  None)# Print size and scale of cipherseal_lib.Ciphertext_Size(  ptr_cipher_res2,  ctypes.byref(cipher_size))seal_lib.Ciphertext_Scale(  ptr_cipher_res2,  ctypes.byref(cipher_scale))print("Size  (before) : {}".format(cipher_size.value))print("Scale (before) : {}".format(math.log(cipher_scale.value, 2)))# Relinearize to reduce the size of a cipher seal_lib.Evaluator_Relinearize(  ptr_evaluator,  ptr_cipher_res2,  ptr_relin_key,  ptr_cipher_res2,  None)# Rescale to set appropriate scaleseal_lib.Evaluator_RescaleToNext(  ptr_evaluator,  ptr_cipher_res2,  ptr_cipher_res2,  None)# Print size and scale of cipherseal_lib.Ciphertext_Size(  ptr_cipher_res2,  ctypes.byref(cipher_size))seal_lib.Ciphertext_Scale(  ptr_cipher_res2,  ctypes.byref(cipher_scale))print("Size  (after) : {}".format(cipher_size.value))print("Scale (after) : {}".format(math.log(cipher_scale.value, 2)))

A cipher text ptr_cipher_res2 and a plain text cannot be added together, since these values have also different levels.
To fix this problem, I apply the following scale setting and modulus switching.

# Normalize scale to 2^40, before adding plaintext 0.5seal_lib.Ciphertext_SetScale(  ptr_cipher_res2,  ctypes.c_double(pow(2.0, 40)))# Get parms idcipher_parms_id = ctypes.c_ulonglong()seal_lib.Ciphertext_ParmsId(  ptr_cipher_res2,  ctypes.byref(cipher_parms_id))# Normalize parameters, before adding plaintext 0.5seal_lib.Evaluator_ModSwitchTo2(  ptr_evaluator,  ptr_plain_05,  ctypes.byref(cipher_parms_id),  ptr_plain_05)

Now we can compute as follows.
The final result will reside in cipher text ptr_cipher_res2.

## Compute 3.14159265 x^3 + 0.5#seal_lib.Evaluator_AddPlain(  ptr_evaluator,  ptr_cipher_res2,  ptr_plain_05,  ptr_cipher_res2)

When I have received this encrypted result, now I can decrypt as follows with secret key.

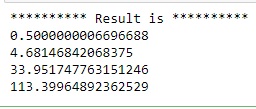
## Decrypt result## Create Decryptorptr_decryptor = ctypes.c_void_p()seal_lib.Decryptor_Create(  ptr_context,  ptr_secret_key,  ctypes.byref(ptr_decryptor))# Create plain text for resultptr_plain_res = ctypes.c_void_p()seal_lib.Plaintext_Create1(  None,  ctypes.byref(ptr_plain_res))# Decrypt resultseal_lib.Decryptor_Decrypt(  ptr_decryptor,  ptr_cipher_res2,  ptr_plain_res)# Decode result with CKKS encoderres_arr = (ctypes.c_double * slot_size.value)()seal_lib.CKKSEncoder_Decode1(  ptr_encoder,  ptr_plain_res,  ctypes.byref(ctypes.c_ulonglong(0)),  ctypes.cast(res_arr, ctypes.POINTER(ctypes.c_double)),  None)# Output resultsprint("********** Result is **********")for i in range(4):  print(res_arr[i])

EVA Compiler (and PyEVA)

As you saw above, programming with primitive SEAL functions is unfriendly for beginners – such as, relinearization, rescaling, and selecting encryption parameters during computations.

That’s why we use EVA compiler, which simplifies CKKS programming in Python language.
EVA compiler will compile your Python code for CKKS scheme, and then you don’t need to operate these laborious tasks by yourself.

Note : In this post, I don’t describe about installing and setting up EVA compiler, but you can refer installation steps in readme.

Now I have re-writed the previous code with EVA compiler as follows.
As you can see below, the programming with EVA compiler (and PyEVA package) is very straightforward. EVA compiler will analyze the formula (3.14159265*x**3 + 0.5) and build computation graph.

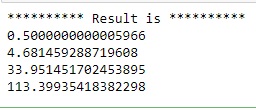
## Define and compile program## Define programfrom eva import *poly = EvaProgram("Polynomial", vec_size=1024)with poly:  x = Input("x")  Output("y", 3.14159265*x**3 + 0.5)poly.set_output_ranges(30)poly.set_input_scales(30)# Compile program with CKKS schemefrom eva.ckks import *compiler = CKKSCompiler()compiled_poly, params, signature = compiler.compile(poly)## Generate key context#   public context contains : public key, relin key, galois key#   secret context contains : secret key#from eva.seal import *public_ctx, secret_ctx = generate_keys(params)## Create encryption for x (= 0.0, 1.1, 2.2, 3.3)#inputs = { "x": [0.0 for i in range(compiled_poly.vec_size)] }inputs["x"][0] = 0.0inputs["x"][1] = 1.1inputs["x"][2] = 2.2inputs["x"][3] = 3.3encInputs = public_ctx.encrypt(inputs, signature)## Execute computation#encOutputs = public_ctx.execute(compiled_poly, encInputs)## Decrypt results#outputs = secret_ctx.decrypt(encOutputs, signature)print("********** Result is **********")for i in range(4):  print(outputs["y"][i])

The generated public context (public_ctx) holds public key, relinearization key (relin key) and galois key (which is used in rotation, such as, Evaluator_RotateVector()), and it can then be shared in public.
On contrary, the secret context (secret_ctx) holds a secret key and this should then be protected in client.

Homomorphic Encryption in Machine Learning (Encrypted Inference)

Now we combine homomorphic encryption and machine learning together.
In machine learning, the prediction (inferencing) in primitive models (which can run with addition and multiplication) can be easily implemented with Microsoft SEAL.

For instance, suppose, we have a model trained by linear regression as follows.
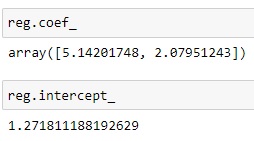
In the following example, we got a model :

for input .

import numpy as npfrom sklearn.linear_model import LinearRegression## Sampling data#np.random.seed(1000) # For debugging and reproducibilityN = 25 * 25x0,x1 = np.mgrid[5.0:5.0 + 0.5 * 25:0.5, 5.0:5.0 + 0.5 * 25:0.5]X = np.vstack((x0.flatten(), x1.flatten())).Ty = x0.flatten() * 5.1 + x1.flatten() * 2.1 + 1.5 + np.random.normal(0.0, 2.0, size=N)## Train with linear regression#reg = LinearRegression().fit(X, y)

Now we can then generate a predictor with Microsoft SEAL as follows.
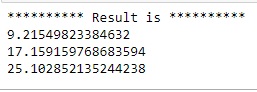
In the following example, we compute for 3 encrypted inputs .

from eva import *from eva.seal import *# Define programpoly = EvaProgram("Polynomial", vec_size=1024)with poly:  x0 = Input("x0")  x1 = Input("x1")  Output("y", reg.coef_[0]*x0 + reg.coef_[1]*x1 + reg.intercept_)poly.set_output_ranges(30)poly.set_input_scales(30)# Compile program with CKKS schemecompiler = CKKSCompiler()compiled_poly, params, signature = compiler.compile(poly)# Generate key contextpublic_ctx, secret_ctx = generate_keys(params)# Create encryption for x0 and x1inputs = { "x0": [0.0 for i in range(compiled_poly.vec_size)], "x1": [0.0 for i in range(compiled_poly.vec_size)] }inputs["x0"][0] = 1.1inputs["x0"][1] = 2.2inputs["x0"][2] = 3.3inputs["x1"][0] = 1.1inputs["x1"][1] = 2.2inputs["x1"][2] = 3.3encInputs = public_ctx.encrypt(inputs, signature)# Compute with homomorphic encryption (HE)encOutputs = public_ctx.execute(compiled_poly, encInputs)# Decrypt resultoutputs = secret_ctx.decrypt(encOutputs, signature)print("********** Result is **********")for i in range(3):  print(outputs["y"][i])# Actual result is 5.1*x0 + 2.1*x1 + 0.5

Note : In practice, you can serialize/deserialize inputs, outputs, and keys by save() / load() functions. See here for example code.

Note : CKKS can directly operate complex values (the number with real part and imaginary part) and you can then seamlessly operate 2-dimensional vectors.

With Azure Machine Learning Python SDK, you can use Python objects (encrypted.inference.eiserver.EIServer, encrypted.inference.eiclient.EILinearRegressionClient) to simplify the encrypted inference in Microsoft SEAL, which is a wrapper function for encrypted dot-product computation. (Currently, in preview. See here.)

Reference :

GitHub – Microsoft SEAL Homomorphic Encryption in Python
https://github.com/tsmatz/homomorphic-encryption-microsoft-seal/