(Download source code from here.)

For the second post in the series, I’ll implement a famous quantum search algorithm, Grover algorithm in Q#.

Series : Quantum algorithm’s implementation (Q#)

• Programming Quantum Algorithm for Beginners (Bernstein-Vazirani algorithm)
• Programming Quantum Search (Grover’s Algorithm)
• Programming Quantum Phase Estimation
• Programming Quantum Arithmetic (Adder, Multiplier, and Exponentiation)
• Programming Quantum Period Finding (Shor’s Algorithm)

What is Grover’s Search algorithm ?

For some , we want to find such as .
In general, the number of solutions can be larger than 1, but here I assume that this equation has a unique solution in order to simplify example.

In the classical approach, it is needed operations (i.e, ) for finding the solutions, however the quantum algorithm (Grover’s search algorithm) needs only for complexity.
As you can see in this post, this Grover’s algorithm might be used for optimizing brute force search to obtain a valid assignment.

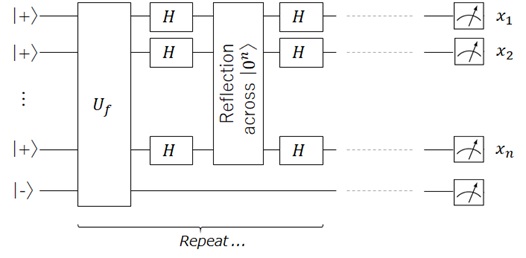
Now I’ll show you the outline of this algorithm. (See “Lecture 6: Quantum Search” (CS 880 – Quantum Information Processing in University of Wisconsin-Madison) for details.)

First we start . As I have mentioned above, only one satisfies , and the other satisfies . Then we assume |〉 can be written as the following format, where |〉 is the transformed state by i iterations. (Later we’ll define this transformation.)

As you can see, and , are then on a unit circle as follows.

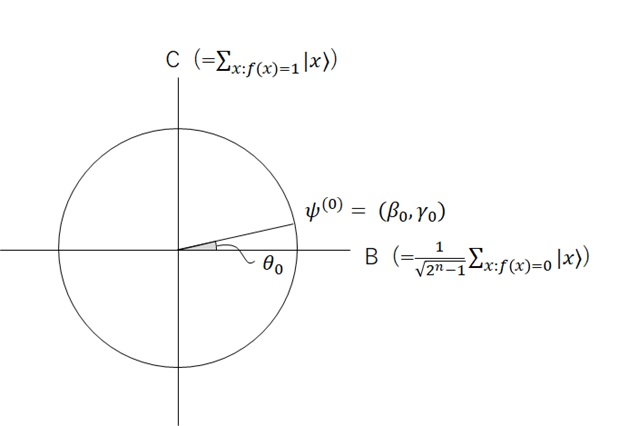
Here we want to try to increase above by iteration i, and if we get sufficiently enough to close C-axis, this state might be close to our expecting solution x. We can then measure x to get a solution.

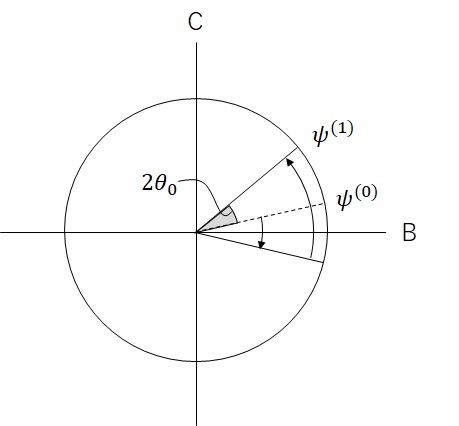
Now we consider the transformation to increase as follows, and we repeat the following 1 and 2. :

1. First, we reflect , across B-axis.
2. Next, we reflect across .

The former one is very easy, because we can use phase kickback (reversible and unitary operation) , which is discussed in my previous post.
As you saw in the previous post, only the item which satisfies is multiplied by . (Otherwise, it’s multiplied by .)

The latter one is a little complicated and here I use the well-known diffusion operator as follows. (Sorry, but I’ll skip the proof, due to avoid description too much …)

where H is Hadamard operation.

As you can see below (by algebraic transformation), this operator is the same as the reflection across average. (See the following illustrated.)

Note : As you can see below, this transformation is also written as : .

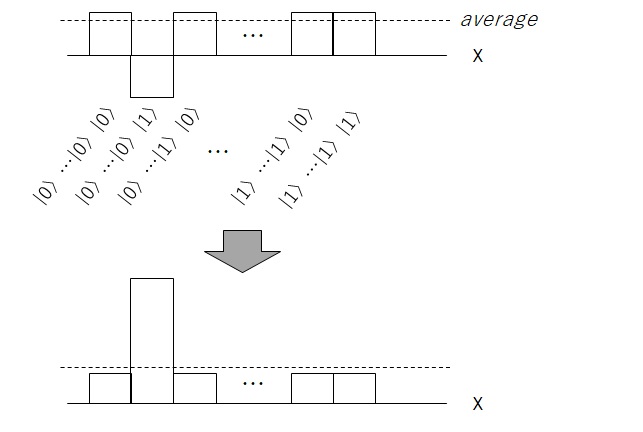
That is, the entire transformation (combination of above #1 and #2) works for amplifying amplitude of the solution of .
We’ll then repeat this transformation until |〉 is close to C-axis.

The entire transformation is designed as follows.

Q# Programming for Grover’s Search algorithm

In this example, we assume is a unique solution for equation .

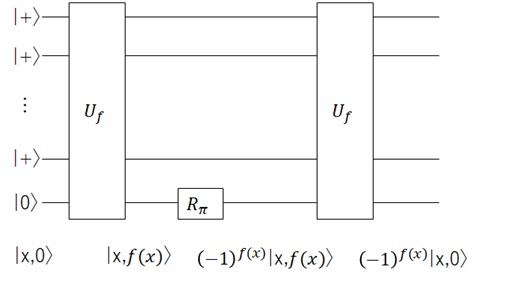
In this implementation, I’ll use phase kickback transformation , instead of .

As I have mentioned in the previous post, the equation (where is implemented by CNOT operation) holds only if , and this equation won’t hold on ancilla qubit .
Thus we use the following transformation instead, which is implemented by the twice and rotation as follows. (See “Lecture 04: Elementary Quantum Algorithms” for details about this circuit.)

Note : is radians rotation about the state (equivalent to rotation in Pauli-Z).
See here for Bloch Sphere representation.

As a result, we will implement the following circuit instead.

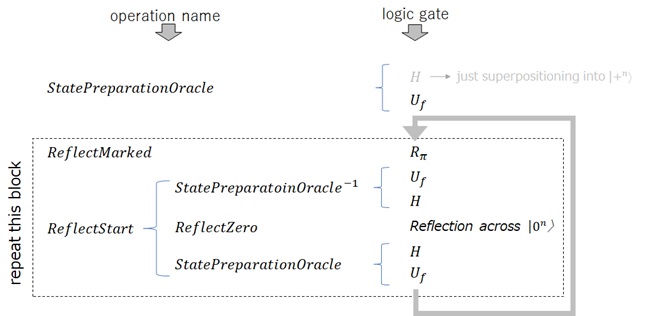
In this example, I’ll build the following operations (StatePreparationOracle(), ReflectMarked(), ReflectStart(), and ReflectZero()) corresponding to each following logics. (Note that is an adjoint conjunction of StatePreparationOracle.)

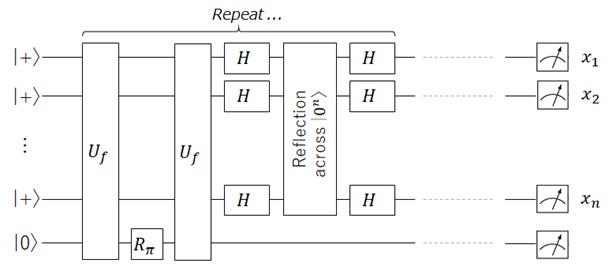
As you can notice, one thing in this flow is different from the original circuit. This circuit has an extra in the final step.
However, this is on purpose. (It has the following meaning.)

By the final (in which, applying conditional for ), the ancilla qubit will become close to if is close to .
Therefore we can figure out whether we could have reached to the solution () by measuring this ancilla qubit. This ancilla qubit is then not a “garbage” qubit.

Now, let’s build Q# code.

First we generate the superposition and (ancilla qubit) as follows. Here () is in “databaseRegister” and ancilla qubit () is in “markedQubit“.
For simplification, we assume n = 6 and the number of iterations is fixed as 3.

nDatabaseQubits = 6;nIterations = 3;use (markedQubit, databaseRegister) = (Qubit(), Qubit[nDatabaseQubits]) {  QuantumSearch(nIterations, markedQubit, databaseRegister);  ...}operation QuantumSearch (nIterations : Int, markedQubit : Qubit, databaseRegister : Qubit[]) : Unit {  StatePreparationOracle(markedQubit, databaseRegister);  ...}operation StatePreparationOracle (markedQubit : Qubit, databaseRegister : Qubit[]) : Unit is Adj + Ctl {  UniformSuperpositionOracle(databaseRegister);  ...}operation UniformSuperpositionOracle (databaseRegister : Qubit[]) : Unit is Adj + Ctl {  body (...) {let nQubits = Length(databaseRegister);for idxQubit in 0 .. nQubits - 1 {  H(databaseRegister[idxQubit]);}  }}

Next we implement by adding DatabaseOracle() operation in StatePreparationOracle() as follows.

By the following “Controlled X(databaseRegister, markedQubit)“, gate X is applied to markedQubit, conditional for all qubits in databaseRegister being in the state. (See the previous post for “Controlled X(a, b)“.)
This entanglement is then equivalent to where has a unique solution for . (Suppose we have blackbox access to this oracle.)

Following “Adj + Ctl” indicates the compiler to implement the adjoint specialization by inverting the body. (Later we’ll use the adjoint operation for StatePreparationOracle, i.e, .)

operation StatePreparationOracle (markedQubit : Qubit, databaseRegister : Qubit[]) : Unit is Adj + Ctl {  UniformSuperpositionOracle(databaseRegister);  DatabaseOracle(markedQubit, databaseRegister);}operation DatabaseOracle (markedQubit : Qubit, databaseRegister : Qubit[]) : Unit is Adj + Ctl {  Controlled X(databaseRegister, markedQubit);}

Now we implement the iteration loop by adding the following code in QuantumSearch().
This logic is equivalent to the repeated block, marked in gray in the following picture.

Let’s see how ReflectZero() operation (reflection across ) is implemented.
I note that the first qubit in argument on ReflectZero() operation is ancilla qubit (markedQubit, which is ) and others are databaseRegister.
The multi-qubit controlled gate “Controlled Z()” will apply Pauli-Z gate conditional on . (See here for Pauli-Z.) Thus we first flip both ancilla qubit (i.e, ) and databaseRegister in ReflectZero(), and then turn into when databaseRegister is . (Finally, we reset ancilla qubit again to .)

Reflection across can also be implemented using with ancilla qubit, where is a function such that is equal to and others are .

operation QuantumSearch (nIterations : Int, markedQubit : Qubit, databaseRegister : Qubit[]) : Unit {  StatePreparationOracle(markedQubit, databaseRegister);  for idx in 0 .. nIterations - 1 {ReflectMarked(markedQubit);ReflectStart(markedQubit, databaseRegister);  }}operation ReflectMarked (markedQubit : Qubit) : Unit {  R1(PI(), markedQubit);}operation ReflectStart (markedQubit : Qubit, databaseRegister : Qubit[]) : Unit {  Adjoint StatePreparationOracle(markedQubit, databaseRegister);  ReflectZero([markedQubit] + databaseRegister);  StatePreparationOracle(markedQubit, databaseRegister);}operation ReflectZero (allQubits : Qubit[]) : Unit {  let nQubits = Length(allQubits);  for idxQubit in 0 .. nQubits - 1 {X(allQubits[idxQubit]);  }  Controlled Z(allQubits[1 .. nQubits - 1], allQubits[0]);  for idxQubit in 0 .. nQubits - 1 {X(allQubits[idxQubit]);  }}

Finally we measure the results as follows.
If it’s succeeded, databaseRegister must be close to (which is a solution for ).
As I have explained above, markedQubit should also be close to on success.

use (markedQubit, databaseRegister) = (Qubit(), Qubit[nDatabaseQubits]) {  QuantumSearch(nIterations, markedQubit, databaseRegister);  // Measure the marked qubit.  // On success, this should be |1〉.  set resultSuccess = M(markedQubit);  // Measure the state of the database register.  // On success, this should be |1〉 |1〉 ... |1〉.  set resultElement = MultiM(databaseRegister);// Reset all qubits to the |0〉 state.  Reset(markedQubit);  for idxResult in 0 .. nDatabaseQubits - 1 {Reset(databaseRegister[idxResult]);  }}

The completed example is below. :
(You can download and run source code from here.)

Q#

open Microsoft.Quantum.Intrinsic;open Microsoft.Quantum.Math;open Microsoft.Quantum.Measurement;operation ApplyQuantumSearch (nIterations : Int, nDatabaseQubits : Int) : (Result, Result[]) {  use (markedQubit, databaseRegister) = (Qubit(), Qubit[nDatabaseQubits]) {QuantumSearch(nIterations, markedQubit, databaseRegister);// Measure the marked qubit.// On success, this should be |1〉.let resultSuccess = M(markedQubit);// Measure the state of the database register.// On success, this should be |1〉 |1〉 ... |1〉.let resultElement = MultiM(databaseRegister);// Reset all qubits to the |0〉 state.Reset(markedQubit);for idxResult in 0 .. nDatabaseQubits - 1 {  Reset(databaseRegister[idxResult]);}return (resultSuccess, resultElement);  }}operation QuantumSearch (nIterations : Int, markedQubit : Qubit, databaseRegister : Qubit[]) : Unit {  StatePreparationOracle(markedQubit, databaseRegister);  for idx in 0 .. nIterations - 1 {ReflectMarked(markedQubit);ReflectStart(markedQubit, databaseRegister);  }}operation StatePreparationOracle (markedQubit : Qubit, databaseRegister : Qubit[]) : Unit is Adj + Ctl{  UniformSuperpositionOracle(databaseRegister);  DatabaseOracle(markedQubit, databaseRegister);}operation UniformSuperpositionOracle (databaseRegister : Qubit[]) : Unit is Adj + Ctl {  body (...) {let nQubits = Length(databaseRegister);for idxQubit in 0 .. nQubits - 1 {  H(databaseRegister[idxQubit]);}  }}operation DatabaseOracle (markedQubit : Qubit, databaseRegister : Qubit[]) : Unit is Adj + Ctl {  Controlled X(databaseRegister, markedQubit);}operation ReflectMarked (markedQubit : Qubit) : Unit {  R1(PI(), markedQubit);}operation ReflectStart (markedQubit : Qubit, databaseRegister : Qubit[]) : Unit {  Adjoint StatePreparationOracle(markedQubit, databaseRegister);  ReflectZero([markedQubit] + databaseRegister);  StatePreparationOracle(markedQubit, databaseRegister);}operation ReflectZero (allQubits : Qubit[]) : Unit {  let nQubits = Length(allQubits);  for idxQubit in 0 .. nQubits - 1 {X(allQubits[idxQubit]);  }  Controlled Z(allQubits[1 .. nQubits - 1], allQubits[0]);  for idxQubit in 0 .. nQubits - 1 {X(allQubits[idxQubit]);  }}

Python (Use Python or .NET)

db_qbit_len = 6;iterations = 3;results = ApplyQuantumSearch.simulate(  nIterations=iterations,  nDatabaseQubits=db_qbit_len)markedQubit = results[0]databaseRegister = results[1]if markedQubit == 1:  print("Succeed !")  print("Found database index : {}".format(databaseRegister))else:  print("Failed !")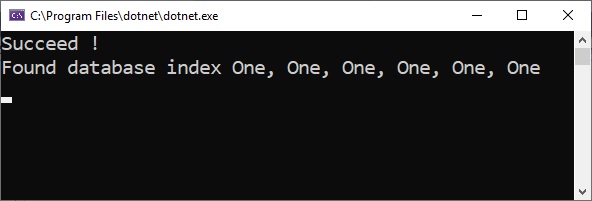

In this post we implemented Grover’s algorithm manually with Q# primitive operators.

However, Q# has built-in Microsoft.Quantum.AmplitudeAmplification.StandardAmplitudeAmplification, which implements the amplitude amplification algorithm, and you’ll be able to implement quantum search algorithm with a few lines of code, using this high-level operation.
Please see StandardAmplitudeAmplification example in official GitHub repository (Microsoft/Quantum).